An essential step in simplifying any algebraic expression is to “combine like terms.” Exactly which terms are “like” in any given expression depends on the type of terms involved: constants, polynomials, radicals, etc.

For example, consider this polynomial expression:

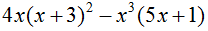
We simplify this expression by performing the given operations and then combining any terms that are “like.” For polynomial expressions, like terms are those having the same degree.

Let’s first perform the operations:

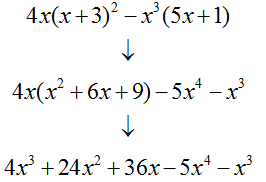
Combining the two like third degree terms, and arranging the expression in descending degree order, we obtain:

The four remaining terms have different exponents and, therefore, are not like terms. They may not be combined.

In our next topic, we will learn to perform the basic operations (addition, subtraction, multiplication, and division) on terms containing radicals, and apply the skill of “combining like terms” to simplify these expressions. .