Multiplying and Dividing Polynomials

Multiplying and Dividing Polynomials – Algebra Tiles

Multiplying and Dividing Polynomials – Algebra TilesAlgebra tiles provide you with the opportunity to use concrete objects to model and perform operations. In this interactivity, you will learn how to use algebra tiles to model and simplify products and quotients of polynomials. Click the player button to begin.

View a printable version of this interactivity.

 

 

Finding Products of Polynomials

Finding Products of PolynomialsIn this interactivity, you will apply your knowledge of the distributive property and combining like terms to determine the products of polynomial expressions. Your knowledge of the properties of exponents will also be useful to you as work through this lesson. Click the player button to begin.

View a printable version of this interactivity.

 

 

FOIL

You have already learned how the distributive property allows you to multiply binomial expressions. The FOIL method is a strategy to help you remember how to apply the distributive property to find the product of binomial expressions. FOIL is an acronym that stands for:

First, Outer, Inner, Last

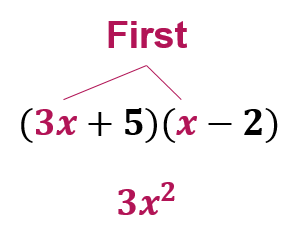
The example below demonstrates how to use the FOIL method to multiply binomials.

(3x + 5)(x − 2)

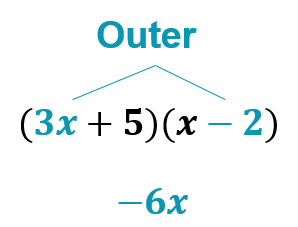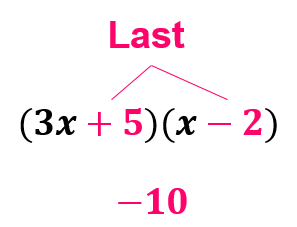By multiplying the first numbers in the binomial, you get three x times x, for a product of three x squared. By multiplying the outer numbers of three x times two, you get a prodcut of six x. By multiplying the inner numbers of five and x, you get a product of five x. By multiplying the last numbers of five and negative two, you get a product of negative ten.

3x2 − 6x + 5x − 10
3x2 − x − 10

 

Special Products

There are patterns that arise when you find the product of certain binomial expressions. These products are referred to as special products. Read through the table below to learn more about special products.

Special Product Example
Perfect Square Trinomial
(m + n)2 = (m + n)(m + n)
  = m2 + mn + mn + n2
  = m2 + 2mn + n2
(x + 5)2 = (x + 5)(x + 5)
  = x2 + 5x + 5x + 25
  = x2 + 10x + 25
(m − n)2 = (m − n)(m − n)
  = m2 − mn − mn + n2
  = m2 − 2mn + n2
(x − 4)2 = (x − 4)(x − 4)
  = x2 − 4x − 4x + 16
  = x2 − 8x + 16
Difference of Squares
(m + n)(m − n) = m2 − mn + mn − n2
  = m2 − n2
(x + 9)(x − 9) = x2 − 9x + 9x − 81
  = = x2 − 81

Practical Problem: Area of a Rectangle

Look at the example below to see how polynomials can be used to model a practical problem.

Example

Wendy has a rectangular-shaped garden. If the width of the garden is two feet more than four times its length, write an expression to represent the garden's area.

rectangular-shaped garden with one side x feet, and the other side four x plus two feet

Area of a rectangle = length x width

  = x(4x + 2)  
  = 4x2 + 2x  

Dividing Polynomial Expressions

Take a moment to look at the example below to see how to use the Quotient of Powers Property to divide polynomial expressions.

Example

Simplify the following expression:

  −40x2 + 24x / 8x  

 
−40x2 + 24x
/8x		 =
−40x2
/8x		 + 24x / 8x  

Consider the expression as the sum of quotients.

  = −5x + 3   Quotient of Powers of Property

 

Multiplying and Dividing Polynomials Review

self-check iconmultiplying and dividing polynomials reviewNow that you have learned about multiplying and dividing polynomials, review your knowledge in this interactivity. Click the player button to get started.

 

 

 

 


Did you answer the content review questions incorrectly? Do you want more instruction or extra practice? If so, view the videos Products of Binomials, Special Products, Modeling Products of Binomials, Products of a Binomial and a Trinomial, and Dividing Polynomials from eMediaVASM.