Rotations

In this video, you will learn about rotations involving a shape turning around a center. You will also consider how the distance from the center to any point on the shape stays the same. Click the player button to begin.

View a transcript of this video.

Solving Rotations Using Formulas

If you prefer a formula-based approach to solving rotations, consider these examples.

Start with the following points:

A(2, 3), B(2, 1), C(4, 2).

After a 90-degree clockwise rotation, where do the points end up? The new points are

A'(3, −2), B'(1, −2), C'(2, −4).

Compare the image to the pre-image. The coordinates went from (x, y) to (y, −x). This will be true for any point rotated 90 degrees clockwise about the origin. These rotations also have an equivalent rotation in the opposite direction. 90 degrees clockwise is the same as 270 degrees counterclockwise.

For a 180-degree clockwise (or counterclockwise) rotation, compare the image points to the pre-image. Again, start with

A(2, 3), B(2, 1), C(4, 2).

After the rotation, the new points are

A"(−2, −3), B"(−2, −1), C"(−4, −2).

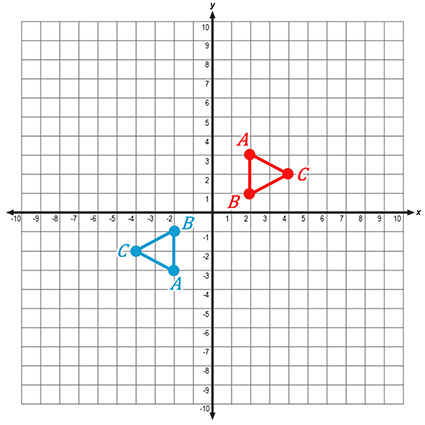Comparing the pre-image to the image, the coordinates changed from (x, y) to (−x, −y). This will be true for any 180-degree rotation about the origin, whether clockwise or counterclockwise.

Now take a look at the 270-degree clockwise rotation. You started with the pre-image points of

A(2, 3), B(2, 1), C(4, 2).

After the rotation, the images are at

A'''(−3, 2), B'''(−1, 2), C'''(−2, 4).

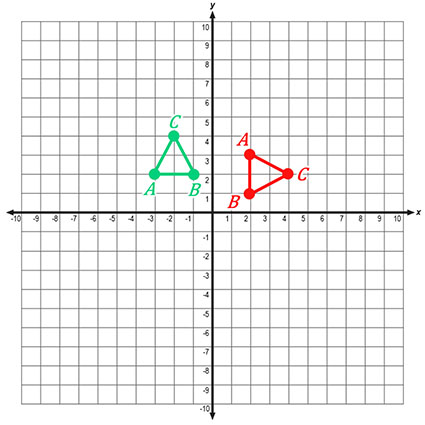The coordinates went from (x, y) to (−y, x). This rotation also has an equivalent rotation in the opposite direction. 270 degrees clockwise is the same as 90 degrees counterclockwise.

 

Rotations Review

Now that you have learned about rotations, review your knowledge in this interactivity. Click the player button to get started.