Universal Gravitation

In 1687, Sir Isaac Newton proposed that every mass in the universe was attracted to every other mass in the universe. The amount of force was directly proportional to the product of the masses of the two objects and inversely proportional to the square of the distance between them. 

This is known as Newton’s Law of Universal Gravitation and today is written as:

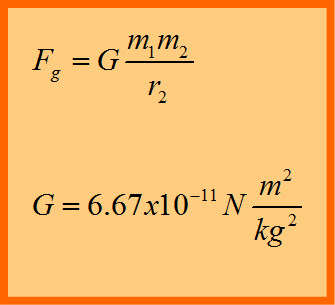
where m one and m two are the masses of the two objects, r is the distance between their centers and G is the universal gravitational constant. 

In standard units, G equals six point six seven times ten to the minus eleven Newtons meters squared per kilogram squared.  The units for the constant simply ensure that when you plug in standard units for the masses and distance, you will wind up with a force in Newtons.

Newton was not actually able to determine the value of the universal gravitational constant.  To determine this constant, Newton needed to know the gravitational acceleration near the surface of the earth, the mass of the earth and the radius of the earth.  Only two of these were known during Newton’s lifetime, the radius of the earth and the gravitational acceleration, so he was left with an equation with two unknowns.

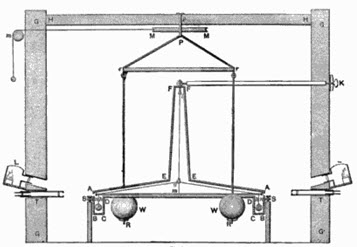
It was over one hundred ten years after Newton proposed the Law of Universal gravitation, that an experiment by Henry Cavendish in 1797 provided a method to determine the gravitational constant, and therefore determine the mass of the earth.

In this lesson, you will combine your knowledge of circular motion with a new topic of universal gravitation. The Law of Universal Gravitation is considered by many to be Newton’s Fourth Law. Click each of the tabsto see Newton's Fourth Law applied. Click the player to begin.

View a printable version of this interactivity.

 

Gravitation Practice

So that you can further develop your skills, you will work through the practice problems, being careful with your use of scientific notation on your calculator. Remember to keep your work well organized. Be sure to try each problem on your own prior to checking each solution. Click the player to begin.