Determining the Slope of a Line
Determining the Slope of a Line When Given an Equation of the Line
When a line is represented as an equation, how can you determine the slope? In this interactivity, you will learn how to determine the slope of a line when given an equation in slope-intercept form, point-slope form, and standard form. Click the player button to begin.
View a printable version of this interactivity.
Determining the Slope of a Line When Given the Graph of the Line
When given the graph of a line, you can use the coordinate plane to determine the slope. Prepare to apply your knowledge of the coordinate plane as you work through this interactivity. Click the player button to begin.
View a printable version of this interactivity.
Slope Formula
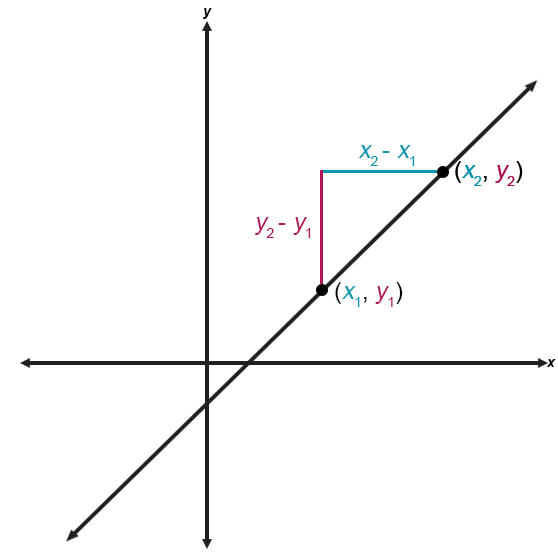
The slope (m) of the line that passes through points (x1, y1) and (x2, y2) is the ratio of the vertical change to the horizontal change.
| slope | = | m | = | vertical changehorizontal change | = | y2 − y1x2 − x1 |
In the following interactivity, you will learn how to use the slope formula to calculate the slope of a line.
Determining the Slope of a Line When Given Two Points on the Line
When given the coordinates of two points on a line, you can use the slope formula to find the slope of the line. Your knowledge of integer operations will be useful as you work through this interactivity. Click the player button to begin.
View a printable version of this interactivity.
Horizontal Lines
In earlier math courses, you learned that a horizontal line has a zero slope and a vertical line has an undefined slope. In the following examples, you will explore how to use the slope formula to confirm these facts.
The equation of a horizontal line is given in the form y = c, where c is a real number.
Below is the graph of the line y = 1:
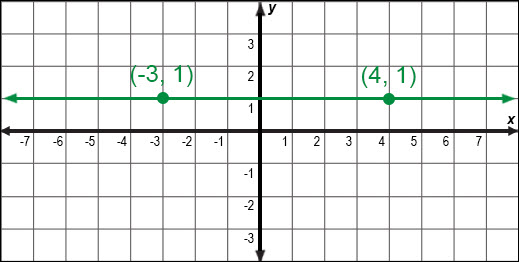
Let (x1, y1) = (−3, 1) and (x2, y2) = (4, 1).
m |
= | y2 − y1x2 − x1 | |
| = | 1 − 14 − (− 3) | Substitute the appropriate values | |
| = | 07 | Simplify the expression | |
| = | 0 |
The slope of the line is zero.
Vertical Lines
The equation of a vertical line is given in the form x = a, where a is a real number.
Below is the graph of the line x = 3:
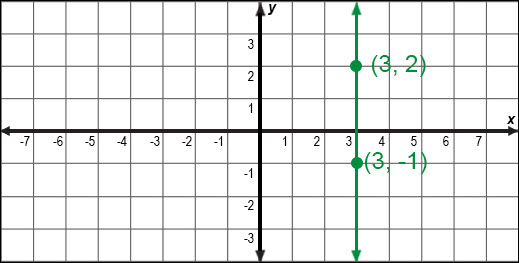
Let (x1, y1) = (3, 2) and (x2, y2) = (3, −1).
m |
= | y2 − y1x2 − x1 | |
| = | −1 − 23 − 3 | Substitute the appropriate values | |
| = | −30 | Simplify the expression |
Division by 0 is undefined. Therefore, the slope of the line is undefined.
Practical Problem
Dana is training for a marathon. While running yesterday, she noted the distance she traveled after running for different periods of time. Her results are represented by the linear function modeled in the table below.
| Time (in minutes) | Distance (in miles) |
|---|---|
| 12 | 1.5 |
| 28 | 3.5 |
| 52 | 6.5 |
Find Dana’s rate of change in distance with respect to time.
The slope of a line represents the constant rate of change in y as x changes by a constant amount; y represents the dependent variable and x represents the independent variable. In this scenario, the distance Dana runs depends on the amount of time she runs. Therefore, the dependent variable y is distance, and the independent variable x is time.
To determine Dana’s rate of change in distance with respect to time, use the slope formula.
Let (x1, y1) = (12, 1.5) and (x2, y2) = (28, 3.5).
m |
= | y2 − y1x2 − x1 | |
| = | 3.5 − 1.528 − 12 | Substitute the appropriate values | |
| = | 216 | Simplify the expression | |
| = | 18 |
By using the slope formula, you find that Dana runs 1 mile every 8 minutes.
Determining the Slope of a Line Review
Now that you have learned how to determine the slope of a line, it is time to test your knowledge. This interactivity will help you review the information covered throughout this topic. Click the player button to get started.
Did you answer the content review questions incorrectly? Do you want more instruction or extra practice? If so, view the videos Calculating the Slope When Given Two Points and Calculating the Slope When Given the Graph of a Line from eMediaVASM.