Quantum Mechanics

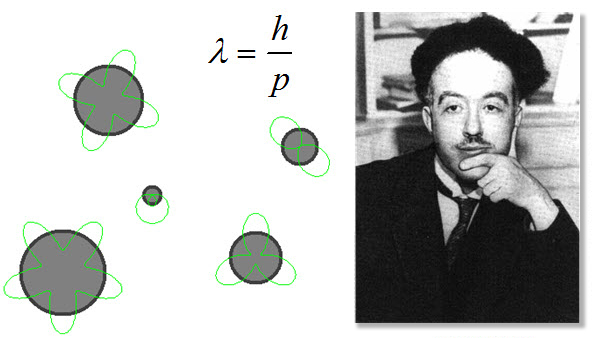
Louis DeBroglie

The Bohr model of the atom left some unanswered questions for scientists. Why didn’t the electrons spiral down toward the nucleus?  Why were the orbits stable? Bohr did not have a reason for this in his model. Louis DeBroglie (pronounced de broy) came up with an idea that would provide an answer to this question in 1924.

From Einstein’s idea of mass and energy equivalence, DeBroglie found a mathematical relationship between wavelength, momentum and Planck’s constant. Wavelength was equal to Planck’s constant divided by the momentum. DeBroglie interpreted this to mean that everything had a wavelength, even material objects like airplanes, bowling balls, or electrons. The wavelength could be calculated using his new equation.  This was revolutionary new idea in physics. 

Once DeBroglie figured out that electrons had wavelengths, he combined this with the physics of standing waves to explain the fixed electron orbits.

DeBroglie’s hypothesis was that there is always an integral number of electron wavelengths around the circumference of each electron orbit.

The standing wave patterns of the electron waves explained why the electrons did not spiral into the nucleus; however, DeBroglie’s theory only worked for hydrogen, not for other atoms.

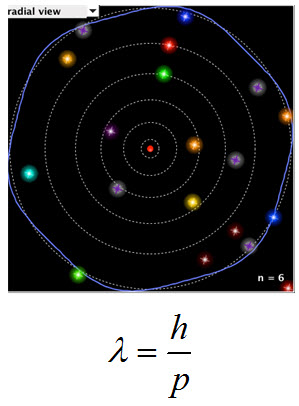In the warm-up you looked at an animation of the DeBroglie model of the atom and compared it to the Bohr model of the atom. 

This snapshot from the simulation is of the n equals six orbital. Count the electron wavelengths. There are six.

 

 

 

 

 

 

 

 

 

The other excited electron states you observed are similar.  Here you can see the  n equals one, two, and four orbitals.  Can you count the wavelengths?

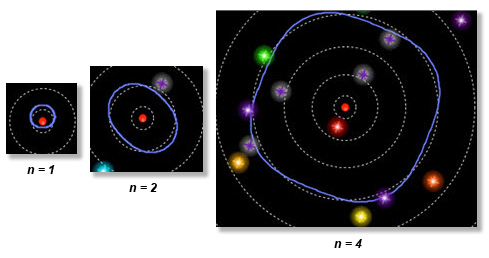
Below are the n equals five and six orbitals.  You should see again that the number of complete wavelengths is equal to the orbital number.

View this video clip on the Particles Waving: The Dual Nature of Light and Matter from Discovery Education^TM streaming to learn more.

With DeBroglie’s theory, matter had both particle and wave properties. Properties of waves include the ability to cause interference. Matter waves can interfere, just like when two light or sound waves interfere and produce constructive or destructive interference effects; however, only very small particles, like those inside an atom, have significant wave properties. 

DeBroglie’s work was theoretical, he had no experimental evidence to support his hypothesis, but three years later, Clinton Davison and Lester Germer discovered that electrons could be diffracted by a nickel crystal. This important discovery provided evidence of the wave nature of matter.

This work won DeBroglie the Nobel Prize in Physics in 1929. 

Since matter has wave properties, this means we can observe interference effects. When laser light is shined through two narrow slits, we see an interference pattern. This is shown on the right. 

The idea that very small particles had wave properties means that we do not really know the precise position of the particle, we know where it is likely to be. In 1926, Werner Heisenberg developed his uncertainty principle. The Heisenberg Uncertainty Principle states that if we try to measure the position of the particle, we lose accuracy in other information about the particle. The more precisely we know its position, the less precisely the momentum can be known. View this video clip on the Elements of Physics: Modern Physics & Cosmology “Quantum Mechanics from Discovery Education^TM streaming to learn more.

In the subatomic world, the classic laws of physics do not apply. Subatomic particles are governed by laws of probability. The branch of physics called quantum mechanics originated in the 1920s. This was a radical new physics, and it was not immediately accepted by all other scientists. Even Einstein had difficulty accepting the idea of using probability in physics. A famous Einstein quote is “God doesn’t play dice.” Einstein argued with Bohr about quantum mechanics; however, all of the predictions of quantum mechanics have been supported by experimental data.

 

Quantum Mechanics Practice

Now that you have explored quantum mechanics, test your knowledge in this non-graded interactivity. Click the player to get started.